Thursday, September 6, 2007

Euclidean space

Euclidean space

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Around 300 BC, the Greek mathematician Euclid laid down the rules of what has now come to be called "Euclidean geometry", which is the study of the relationships between angles and distances in space. Euclid first developed "plane geometry" which dealt with the geometry of two-dimensional objects on a flat surface. He then went on to develop "solid geometry" which analyzed the geometry of three-dimensional objects. All of the axioms of Euclid have been encoded into an abstract mathematical space known as a two- or three-dimensional Euclidean space. These mathematical spaces may be extended to apply to any dimension, and such a space is called an n-dimensional Euclidean space or an n-space. This article is concerned with such mathematical spaces.

In order to develop these higher dimensional Euclidean spaces, the properties of the familiar Euclidean spaces must be very carefully expressed and then extended to an arbitrary dimension. Although the resulting mathematics is rather abstract, it nevertheless captures the essential nature of the Euclidean spaces we are all familiar with.

An essential property of a Euclidean space is its flatness. Other spaces exist that are not Euclidean. For example, the surface of a sphere is not a Euclidean space, nor is the four-dimensional spacetime described by the theory of relativity when gravity is present. The geometry of such spaces is called non-Euclidean geometry.

In theoretical physics, the term Euclidean space is usually in the context of being compared to Minkowski space. While a Euclidean space has only spacelike dimensions, a Minkowski space has also one timelike dimension. Therefore the symmetry group of a Euclidean space is the rotation group and for a Minkowski space it is the Lorentz group.

Contents

[hide]

[edit] Intuitive overview

One way to think of the Euclidean plane is as a set of points satisfying certain relationships, expressible in terms of distance and angle. For example, there are two fundamental operations on the plane. One is translation, which means a shifting of the plane so that every point is shifted in the same direction and by the same distance. The other is rotation about a fixed point in the plane, in which every point in the plane turns about that fixed point through the same angle. One of the basic tenets of Euclidean geometry is that two figures (that is, subsets) of the plane should be considered equivalent (congruent) if one can be transformed into the other by some sequence of translations and rotations. (See Euclidean group.)

In order to make all of this mathematically precise, one must clearly define the notions of distance, angle, translation, and rotation. The standard way to do this, as carried out in the remainder of this article, is to define the Euclidean plane as a two-dimensional real vector space equipped with an inner product. For then:

  • the vectors in the vector space correspond to the points of the Euclidean plane,
  • the addition operation in the vector space corresponds to translation, and
  • the inner product implies notions of angle and distance, which can be used to define rotation.

Once the Euclidean plane has been described in this language, it is actually a simple matter to extend its concept to arbitrary dimensions. For the most part, the vocabulary, formulas, and calculations are not made any more difficult by the presence of more dimensions. (However, rotations are more subtle in high dimensions, and visualizing high-dimensional spaces remains difficult, even for experienced mathematicians.)

A final wrinkle is that Euclidean space is not technically a vector space but rather an affine space, on which a vector space acts. Intuitively, the distinction just says that there is no canonical choice of where the origin should go in the space, because it can be translated anywhere. In this article, this technicality is largely ignored.

[edit] Real coordinate space

Let R denote the field of real numbers. For any non-negative integer n, the space of all n-tuples of real numbers forms an n-dimensional vector space over R, which is denoted Rn and sometimes called real coordinate space. An element of Rn is written

x = (x1, x2, …, xn),

where each xi is a real number. The vector space operations on Rn are defined by

\mathbf{x} + \mathbf{y} = (x_1 + y_1, x_2 + y_2, \ldots, x_n + y_n),
a\,\mathbf{x} = (a x_1, a x_2, \ldots, a x_n).

The vector space Rn comes with a standard basis:

\mathbf{e}_1 = (1, 0, \ldots, 0),
\mathbf{e}_2 = (0, 1, \ldots, 0),
\vdots
\mathbf{e}_n = (0, 0, \ldots, 1).

An arbitrary vector in Rn can then be written in the form

\mathbf{x} = \sum_{i=1}^n x_i \mathbf{e}_i.

Rn is the prototypical example of a real n-dimensional vector space. In fact, every real n-dimensional vector space V is isomorphic to Rn. This isomorphism is not canonical, however. A choice of isomorphism is equivalent to a choice of basis for V (by looking at the image of the standard basis for Rn in V). The reason for working with arbitrary vector spaces instead of Rn is that it is often preferable to work in a coordinate-free manner (that is, without choosing a preferred basis).

[edit] Euclidean structure

Euclidean space is more than just a real coordinate space. In order to apply Euclidean geometry one needs to be able to talk about the distances between points and the angles between lines or vectors. The natural way to obtain these quantities is by introducing and using the standard inner product (also known as the dot product) on Rn. The inner product of any two vectors x and y is defined by

\mathbf{x}\cdot\mathbf{y} = \sum_{i=1}^n x_iy_i = x_1y_1+x_2y_2+\cdots+x_ny_n.

The result is always a real number. Furthermore, the inner product of x with itself is always nonnegative. This product allows us to define the "length" of a vector x as

\|\mathbf{x}\| = \sqrt{\mathbf{x}\cdot\mathbf{x}} = \sqrt{\sum_{i=1}^{n}(x_i)^2}.

This length function satisfies the required properties of a norm and is called the Euclidean norm on Rn.

The (non-obtuse) angle θ (0° ≤ θ ≤ 180°) between x and y is then given by

\theta = \cos^{-1}\left(\frac{\mathbf{x}\cdot\mathbf{y}}{\|\mathbf{x}\|\|\mathbf{y}\|}\right)

where cos−1 is the arccosine function.

Finally, one can use the norm to define a metric (or distance function) on Rn by

d(\mathbf{x}, \mathbf{y}) = \|\mathbf{x} - \mathbf{y}\| = \sqrt{\sum_{i=1}^n (x_i - y_i)^2}.

This distance function is called the Euclidean metric. It can be viewed as a form of the Pythagorean theorem.

Real coordinate space together with this Euclidean structure is called Euclidean space and often denoted En. (Many authors refer to Rn itself as Euclidean space, with the Euclidean structure being understood). The Euclidean structure makes En an inner product space (in fact a Hilbert space), a normed vector space, and a metric space.

Rotations of Euclidean space are then defined as orientation-preserving linear transformations T that preserve angles and lengths:

T\mathbf{x} \cdot T\mathbf{y} = \mathbf{x} \cdot \mathbf{y},
|T\mathbf{x}| = |\mathbf{x}|.

In the language of matrices, rotations are special orthogonal matrices.

[edit] Topology of Euclidean space

Since Euclidean space is a metric space it is also a topological space with the natural topology induced by the metric. The metric topology on En is called the Euclidean topology. A set is open in the Euclidean topology if and only if it contains an open ball around each of its points. The Euclidean topology turns out to be equivalent to the product topology on Rn considered as a product of n copies of the real line R (with its standard topology).

An important result on the topology of Rn, that is far from superficial, is Brouwer's invariance of domain. Any subset of Rn (with its subspace topology) that is homeomorphic to another open subset of Rn is itself open. An immediate consequence of this is that Rm is not homeomorphic to Rn if m ≠ n — an intuitively "obvious" result which is nonetheless difficult to prove.

[edit] Relation to manifolds

In modern mathematics, Euclidean spaces form the prototypes for other, more complicated geometric objects. In particular, a manifold is a Hausdorff topological space that is locally homeomorphic to Euclidean space.

Euclidean n-space is the most elementary example of an n-dimensional manifold. In fact, it is a smooth manifold. For n ≠ 4, any differentiable n-manifold that is homeomorphic to Rn is also diffeomorphic to it. The surprising fact that this is not true for n = 4 was proved by Simon Donaldson in 1982; the counterexamples are called exotic (or fake) 4-spaces.

Furthermore, Euclidean space is a linear manifold. An m-dimensional linear submanifold of Rn is a Euclidean space of m dimensions embedded in it (as an affine subspace). For example, any straight line in some higher-dimensional Euclidean space is a 1-dimensional linear submanifold of that space.

In general, the notion of manifolds embraces both Euclidean and non-Euclidean geometry. From this point of view, the essential property of Euclidean space is that it is flat — that is, not curved. Modern physics, specifically the theory of relativity, demonstrates that our universe is not truly Euclidean. Although this is significant in theory and even in some practical problems, such as global positioning and airplane navigation, a Euclidean model can still be used to solve many other practical problems with sufficient precision.

[edit] See also

[edit] References

Retrieved from "http://en.wikipedia.org/wiki/Euclidean_space"
Posted by at

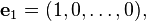
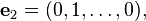
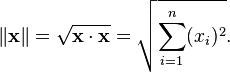
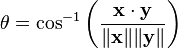
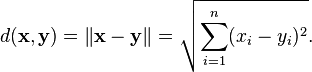
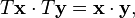
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)